The ACT® WorkKeys applied mathematics test is one of the 8 sections of the ACT WorkKeys test, an assessment tool that evaluates work-related skills and job performance. This section measures your mathematical reasoning, problem-solving ability, and critical thinking.
Passing the applied mathematics section of the test is essential for receiving the National Career Readiness Certificate (NCRC).
The following page will give you the information and practice needed to ace the ACT WorkKeys applied mathematics test, with sample questions, detailed answers, and preparation tips.
Scoring high on the WorkKeys test will demand a strong grip at several mathematics levels, requiring proper practice and guidance. Make sure to check our:
ACT WorkKeys Test Guide and Practice • Free WorkKeys Practice Test
What Is the WorkKeys Applied Mathematics Test?
The ACT WorkKeys applied math test assesses numerical reasoning and problem-solving techniques required in the workplace. As such, the questions are based on real-life scenarios that employees experience daily.
The test has 5 difficulty levels, ranging from 3 to 7. The levels are built on top of one another, each incorporating the skills assessed in the previous level. Thus, in level 6, you will need the skills from levels 4 and 5.
You will have 55 minutes to answer 34 questions.
You are allowed to use a calculator and the ACT WorkKeys formula sheet.
This section of the WorkKeys test can be administered by computer or pencil-and-paper, depending on the testing center you registered at.
If you're looking for free practice, you can check our Free Workkeys Practice Test.

WorkKeys Applied Mathematics Test – Level 3 Questions
In level 3 of the WorkKeys applied math test, you will be presented with word problems that need to be translated into math equations. You will be given all the information you need in a logical order, and you will need to demonstrate numerical skills such as converting fractions and converting between decimals and percentages.
- Solving problems that require one type of operation, such as adding and subtracting
- Converting fractions
- Converting between decimals and percentages
- Converting units
- Adding prices to products and calculating the change
Let's see how it looks –
WorkKeys Applied Mathematics Test Level 3
Practice Question #1
Three elephants drank 250 gallons of water in two days. Elephant A drank the same amount of water each day. On the second day, Elephant B drank three gallons less than on the first day, and elephant C drank three gallons more than on the first day. How many gallons did the elephants drink on the second day?
In order to figure out how many gallons the elephants drank on the second day, first sum up the information:
| Elephant A | Elephant B | Elephant C |
|---|---|---|
| A | B | C |
| A | B-3 | C+3 |
Add the gallons each drank on the two days:

The elephants drank 250 gallons in two days; accordingly:

Note that the three extra gallons that elephant C drank on the second day cancel out the three fewer gallons Elephant B drank on the second day. Thus, together, the three elephants drank the same amount of water on the first day as on the second. If you have keen enough mathematical intuition, you may have noticed this without having to use any equations at all, but if you did use math - don't worry, this is how those instincts are developed.
If you chose answers (A) or (C), review the given information and check for differences. If you chose answer (D), you may have calculated the total amount of water the elephants drank on those two days.
The correct answer is B
WorkKeys Applied Mathematics Test Level 3
Practice Question #2
A college fraternity planned a three-day study marathon. On the first day, they studied 75% of the time, ate for 3 hours, and slept the rest of the time. On the second day, they studied 50% of the time, ate for 4 hours, and slept the rest of the time. On the third day, they slept 1⁄3 of the time. How many hours in total did the fraternity members sleep during the three days?
Note that one day contains 24 hours.
Calculate the number of hours the fraternity slept every day:
Start by converting the percentages into absolute hours.
First day (24 hours):
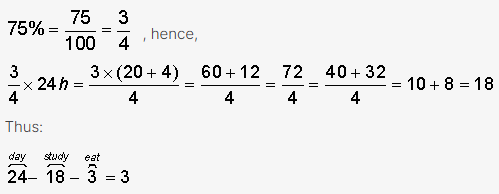
The students slept for 3 hours on the first day.

Total number of hours spent in sleep: 3+8+8 = 19
The correct answer is B
WorkKeys Applied Mathematics Test – Level 4 Questions
In addition to the type of questions you answered in level 3, you will be presented with questions in which the information can be out of order or include extra and unnecessary information and questions, which can include graphs. You will need to demonstrate numerical skills such as evaluating ratios, rates, and proportions, and calculating averages of a set of numbers.
- Solving problems that require two mathematical operations
- Calculating averages and means of a set of numbers
- Evaluating ratios, rates, and proportions
- Adding and subtracting fractions with a common denominator
- Multiplying mixed numbers by whole numbers or decimals
- Organizing information in the correct order before calculating
Let's check it out –
WorkKeys Applied Mathematics Test Level 4
Practice Question #1
Dan took a two-hour walk around a round lake. The radius of the lake is 6 feet. What was Dan's average speed?
Any time we need to calculate the speed, we should use the formula time x speed = distance:
The time is given. Now, in order to calculate the speed, first find the distance.
The lake is round with a radius of 6 feet. Accordingly, if Dan took a walk around the lake, the distance he walked is also the perimeter of the lake.
Therefore, use the formula of a circle’s perimeter in order to calculate the perimeter of the lake:

Therefore, Dan's average speed is 6π.
If you chose any other answer, review the solution and your calculations.
The correct answer is B
WorkKeys Applied Mathematics Test Level 4
Practice Question #2
The ingredients for a barrel of moisturizer are: 7⁄8 of a gallon glycerin, 1⁄4 of a gallon alcohol, 3⁄4 of a gallon fruit oil, and 4⁄32 of a gallon fragrance. In the perfume shop, the workers divided 7 barrels into 70 bottles. After a week, 52 bottles remained unsold. From the remaining bottles, the workers created 70 cream jars.
What is the moisturizer volume of one jar of cream?
Calculate the volume of one barrel by using 32 as a common denominator:

The volume of a single barrel is, therefore, 2 gallons.
Next, calculate the amount of moisturizer in each jar according to the given information.
First step:

A jar contains 52⁄350 of a gallon.
If you chose answer (D), review your calculations. If you chose answers (A) or (C), review your calculations of the transition process from a barrel to a jar.
The correct answer is B
WorkKeys Applied Mathematics Test – Level 5 Questions
In addition to the type of questions you answered in levels 3 and 4, you will be presented with questions that may require several calculations and logical steps. You will need to demonstrate numerical skills such as adding and subtracting fractions with different denominators and calculating percentages.
- Deciding which information, calculations, and conversions to use to solve the problem
- Adding and subtracting fractions with different denominators
- Converting units within and between systems of measurements
- Solving problems with mixed units
- Calculating perimeters, areas, and circumferences of shapes
- Calculating percentages
- Identifying mistakes in calculations
Let's view practice questions –
WorkKeys Applied Mathematics Test Level 5
Practice Question #1
There are 25 monkeys in the zoo. The average weight of 5 of those monkeys is 100 pounds, and the average weight of the rest of them is 75 pounds. What is the average weight of all the monkeys in the zoo in pounds?
First, summarize the given information:
5 monkeys 🠖 100 lb per monkey, on average.
25-5 = 20 monkeys 🠖 75 lb per monkey, on average.
In order to find the average weight of all the monkeys in the zoo, calculate the total weight of all the monkeys:

Next, in order to calculate the average, substitute the total weight in the formula:

The average weight of all the monkeys in the zoo is 80 lb.
If you chose any other answer, check your calculations.
The correct answer is A
WorkKeys Applied Mathematics Test Level 5
Practice Question #2
A pencil is sketched using a rectangle and an isosceles triangle. The length of the pencil is 12 inches. The length of the rectangular section is five times longer than its width, and the height of the triangle is 2 inches. What is the perimeter of the pencil?

In order to solve this problem, calculate the length of all outer sides of both the rectangle and the triangle.
From the given information, it is known that the total length of the pencil is 12 inches, and the height of the triangle is 2 inches; therefore, the length of one side of the rectangle is: 12-2 = 10 inches.
Given that one side of the rectangle is five times longer than the other:

And, since opposite sides of a rectangle have the same length (or “congruent”):

In an isosceles triangle, the height is perpendicular to the base and divides the base into two equal parts, thus the sides of the triangle can be calculated using the Pythagorean Theorem:

The perimeter of the pencil is:
inches.
If you chose answer (A), you probably confused the base and the other sides of the triangle. If you chose answer (C), you probably forgot to divide the base by two, and if you chose answer (D), review the solution.
The correct answer is B
WorkKeys Applied Mathematics Test – Level 6 Questions
In addition to the type of questions you answered in levels 3 to 5, you will be presented with questions that may require translation from verbal to mathematical expression and multiple-step calculations. You will need to demonstrate numerical skills such as calculating reverse percentages and converting units within and between systems of measurement.
- Using fractions with different denominators
- Calculating reverse percentages
- Converting units within and between systems of measurements using multi-step calculations
- Identifying mistakes in solutions
- Finding the area of shapes by converting measurements and units and rearranging formulas
- Calculating the volume of rectangular solids
- Calculating rates, productions rates, and rates by time
- Identifying the correct equation to solve a question
Let's solve some practice questions –
WorkKeys Applied Mathematics Test Level 6
Practice Question #1
Boston Fall is a new self-service salad restaurant. Dan went to the restaurant and asked for half a cucumber, one large potato, two carrots, three onions, three tomatoes, and one corncob.
The cost of one cucumber is a dollar; one large potato is 1⁄2 a dollar; one carrot is 3⁄4 of a dollar; one onion is 1⁄8 of a dollar; one tomato is 2 1⁄3 dollars; and one corncob is 3⁄8 of a dollar.
Dan came back with two friends: Michael asked for the same ingredients in his salad but with half the amount of each vegetable, and Brian asked for the same ingredients but with triple the amount of each vegetable. Dan offered to pay for everything.
What is the difference between the price Dan paid for the three salads and the price Dan would have paid for his salad only?
Summarize the information given:
| Quantity | Vegetable | Price for One ($) | Paid in Total ($) |
|---|---|---|---|
| ½ | Cucumber | 1 | ½ |
| 2 | Carrot | ¾ | ¾ × 2 = ¾ ⅔ = 1 ½ |
| 1 | Potato | ½ | ½ |
| 3 | Onion | ⅛ | ⅛ × 3 = ⅜ |
| 3 | Tomato | 2 ⅓ | 2 ⅓ × 3 ⅔ × 3 = 7 |
| 1 | Corncob | ⅜ | ⅜ |
Calculate the price of Dan's salad:

Michael ordered half the amount of vegetables as Dan:

Brian ordered three times the amount of vegetables as Dan:

Instead of Dan paying only for his salad,
Dan paid for Dan's + Michael's + Brian's salad.
Therefore, the difference in cost is Michael's salad plus Brian's salad:

The difference between the price Dan paid and the price he would have paid for his salad alone is 35 7⁄8.
If you chose (A), you probably forgot to calculate the tomatoes. If you chose answer (B), you probably did not add up the vegetables correctly. If you chose answer (C), review your calculations.
The correct answer is D
WorkKeys Applied Mathematics Test Level 6
Practice Question #2
Dan is diving in El-Nido in the Philippines. He starts his dive from a boat five meters above sea level (0 meters), and he is descending two meters each minute.
Which of the following describes Dan’s dive as a function of elevation and time?
The line equation: y = mx + n;
m = slope,
n = the intersection point between the line and the y-axis.
The graph is the elevation of Dan relative to the ground as a function of time. The x-axis represents time. The y-axis represents elevation; Dan was five meters above when he dove: i.e he had an elevation of 5 meters, at time = 0 minutes. Therefore, the beginning point is (0, 5).
Dan is diving down at a rate of two meters per minute. This means that the slope is: m = -2 meters/minute
Find the linear equation describing Dan’s dive, using the information you found:

Now find another one or two points and find a graph that maintains these points:

The only graph containing these points is A.
If you chose answer (B), note that the graph starts at the origin. If you chose answer (C), note that the graph’s slope is -1. If you chose answer (D), note that the graph’s slope is -1, and it starts at the origin.
The correct answer is A
Create Your Own Assessment Prep Kit!
Finding a job can be a lengthy and challenging journey, often stretching over months and requiring multiple pre-employment tests and interviews. With our Premium Membership, you'll have the support you need every step of the way.
Mix & match 3 Preparation Packs at 50% discount for 1,3, or 6 months
WorkKeys Applied Mathematics Test – Level 7 Questions
In addition to the type of questions you answered in levels 3 to 6, you will be presented with questions with missing or implicit information. You will need to demonstrate numerical skills such as converting between units of measurement using fractions, decimals, and percentages and calculating the volumes of cones, spheres, and cylinders.
- Solving fraction problems that include rates, ratios, and proportions
- Identifying the reason for a mistake
- Converting between units of measurement using percentages, decimals, fractions, and mixed numbers
- Calculating the volumes of cylinders, cones, and spheres
- Calculating volumes by converting units and rearranging formulas
- Manipulating and arranging fractions-related rates, rations, and proportions
- Determining the preferred economic value of alternatives by using graphics, interpreting the measurements of tolerance and spread, and determining percentage differences.
Let's see how it looks –
WorkKeys Applied Mathematics Test Level 7
Practice Question #1
Nancy is planning a ring-shaped pool for a new hotel in Florida. The outer diameter of the pool is 100 feet. If the pool has an area of square 1600π ft., which of the following is its inner diameter (the diameter of the dry area)?

Remember that
The outer diameter is 100 feet. Therefore, the radius of the entire shape is 50:

The total area of the pool is the area of the whole shape minus the dry area (da):

The length of a radius can be only positive; therefore, r = 30.
The diameter (d) equals two times the radius:
d = 2r = 2x30 = 60.
The inner diameter is 60 ft. If you chose any other answer, review your solution.
The correct answer is A
WorkKeys Applied Mathematics Test Level 7
Practice Question #2
Twenty gallons of olive oil were poured into two containers of different sizes. g gallons were poured into the larger container and the rest into the smaller container. The smaller container was then divided equally into two cans, labeled can A and can B.
Dan added
gallons of olive oil to can B.
Express the amount of olive oil in can B after the addition.
First, calculate the amount of olive oil in each container:
Large container: g gallons.
Small container: 20 - g gallons.
Next, calculate the amount in cans A and B:
Express the amount of olive oil in can B after the addition of (g⁄2)2

Simplify:

The amount of olive oil in can B after the addition is:
If you chose answers (A) or (B), you probably expressed the amount of oil in the small container as g. If you chose answer (C), you probably calculated the oil addition incorrect.
The correct answer is D
Think you got it? Check out our full WorkKeys practice test
---
JobTestPrep's WorkKeys assessment test PrepPack, walks you through practice tests from level 3 to 7, sharpening the specific skills for each level.
Learn more about JobTestPrep's WorkKeys assessment test PrePack
WorkKeys Applied Mathematics Test Solving and Preparation Tips

If you don’t know the answer, guess!
The WorkKeys Applied Mathematics Test score is based on the number of correct answers and is not reduced by incorrect answers. So, if you can't figure it out, you can guess and move on.

Read the questions carefully
Ensure you read the question with extra attention, especially at the higher difficulty levels, where deliberately unnecessary and misleading information is designed to distract you.

Use every means necessary
You are allowed to use a calculator and a formula sheet. Even if you can reach the answer on your own, you still have limited time, and as the test goes on, it becomes more difficult. So don't waste your time on the first levels; you will need it later.

Prepare for the right questions
The WorkKeys Applied Mathematics test has particular numerical problems that assess your work-related skills. Thus, you should prepare for these questions and not waste your energy on generic numerical reasoning practice tests, which may be good for general numerical practice but not for what you ware likely to encounter on this test.
JobTestPrep's WorkKeys assessment test PrepPack will provide you with all the tools needed to ace each of the 7 levels of the WorkKeys Applied Math test.
Or read more about our ACT WorkKeys Preparation Pack




